There are two summary functions included with the rCISSVAE package that can help visualize the data clusters and model suitability to the data.
Per-cluster Summary
The cluster_summary() function creates a data summary
table stratified by missingness cluster. The function builds on
gtsummary::tbl_summary(), so gtsummary-like statistics can
be used for summarizing variables
(
see tbl_summary() documentation for details ).
## ── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
## ✔ dplyr 1.1.4 ✔ readr 2.1.5
## ✔ forcats 1.0.0 ✔ stringr 1.6.0
## ✔ ggplot2 4.0.1 ✔ tibble 3.3.0
## ✔ lubridate 1.9.4 ✔ tidyr 1.3.2
## ✔ purrr 1.2.0
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## ✖ dplyr::filter() masks stats::filter()
## ✖ dplyr::lag() masks stats::lag()
## ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors##
## Attaching package: 'kableExtra'
##
## The following object is masked from 'package:dplyr':
##
## group_rows
library(gtsummary)
data(df_missing)
data(clusters)
## Integer clusters must be passed in as a factor
cluster_summary(data = df_missing, factor(clusters$clusters),
include = setdiff(names(df_missing), "index"),
statistic = list(
all_continuous() ~ "{mean} ({sd})",
all_categorical() ~ "{n} / {N}\n ({p}%)"),
missing = "always")| Characteristic | N |
0 N = 2,0001 |
1 N = 2,0001 |
2 N = 2,0001 |
3 N = 2,0001 |
|---|---|---|---|---|---|
| Age | 8,000 | 10.10 (2.04) | 10.19 (2.08) | 10.21 (2.14) | 10.29 (2.06) |
| Unknown | 0 | 0 | 0 | 0 | |
| Salary | 8,000 | 5.81 (0.61) | 5.83 (0.62) | 5.83 (0.61) | 5.81 (0.60) |
| Unknown | 0 | 0 | 0 | 0 | |
| ZipCode10001 | 8,000 | 646 / 2,000 (32%) | 674 / 2,000 (34%) | 663 / 2,000 (33%) | 645 / 2,000 (32%) |
| Unknown | 0 | 0 | 0 | 0 | |
| ZipCode20002 | 8,000 | 703 / 2,000 (35%) | 652 / 2,000 (33%) | 655 / 2,000 (33%) | 687 / 2,000 (34%) |
| Unknown | 0 | 0 | 0 | 0 | |
| ZipCode30003 | 8,000 | 651 / 2,000 (33%) | 674 / 2,000 (34%) | 682 / 2,000 (34%) | 668 / 2,000 (33%) |
| Unknown | 0 | 0 | 0 | 0 | |
| Y11 | 4,878 | -21 (10) | -16 (9) | 8 (5) | -3 (6) |
| Unknown | 1,281 | 1,288 | 0 | 553 | |
| Y12 | 4,882 | 69 (11) | -26 (9) | 55 (6) | -24 (8) |
| Unknown | 1,264 | 1,283 | 0 | 571 | |
| Y13 | 4,890 | 77 (12) | -25 (9) | 98 (12) | -17 (7) |
| Unknown | 1,289 | 1,264 | 0 | 557 | |
| Y14 | 4,871 | 73 (12) | -21 (8) | 125 (16) | -11 (6) |
| Unknown | 1,300 | 1,283 | 0 | 546 | |
| Y15 | 4,859 | 76 (12) | -12 (6) | 141 (19) | -14 (6) |
| Unknown | 1,273 | 1,293 | 0 | 575 | |
| Y21 | 4,865 | -33 (12) | -28 (11) | 1 (7) | -12 (7) |
| Unknown | 1,266 | 1,292 | 0 | 577 | |
| Y22 | 4,906 | 69 (12) | -40 (12) | 54 (6) | -36 (10) |
| Unknown | 1,266 | 1,276 | 0 | 552 | |
| Y23 | 4,902 | 79 (13) | -38 (11) | 104 (13) | -29 (9) |
| Unknown | 1,273 | 1,275 | 0 | 550 | |
| Y24 | 4,854 | 75 (12) | -32 (10) | 135 (18) | -22 (7) |
| Unknown | 1,302 | 1,287 | 0 | 557 | |
| Y25 | 4,894 | 78 (13) | -22 (8) | 153 (21) | -25 (8) |
| Unknown | 1,257 | 1,294 | 0 | 555 | |
| Y31 | 5,933 | -18 (10) | -13 (9) | 13 (5) | 1 (6) |
| Unknown | 192 | 1,285 | 0 | 590 | |
| Y32 | 5,944 | 74 (11) | -24 (10) | 62 (7) | -21 (8) |
| Unknown | 206 | 1,287 | 0 | 563 | |
| Y33 | 5,987 | 84 (13) | -23 (10) | 108 (13) | -14 (7) |
| Unknown | 203 | 1,267 | 0 | 543 | |
| Y34 | 5,949 | 81 (13) | -17 (8) | 136 (17) | -7 (6) |
| Unknown | 195 | 1,275 | 0 | 581 | |
| Y35 | 5,946 | 83 (13) | -8 (6) | 153 (20) | -10 (7) |
| Unknown | 204 | 1,285 | 0 | 565 | |
| Y41 | 5,968 | -8 (4) | -5 (3) | 6 (2) | 1 (2) |
| Unknown | 184 | 1,279 | 0 | 569 | |
| Y42 | 5,978 | 35 (6) | -11 (4) | 29 (4) | -9 (3) |
| Unknown | 199 | 1,282 | 0 | 541 | |
| Y43 | 5,987 | 39 (7) | -10 (3) | 49 (6) | -6 (3) |
| Unknown | 217 | 1,242 | 0 | 554 | |
| Y44 | 5,977 | 37 (7) | -8 (3) | 62 (9) | -3 (2) |
| Unknown | 186 | 1,280 | 0 | 557 | |
| Y45 | 5,914 | 39 (7) | -4 (3) | 70 (10) | -5 (2) |
| Unknown | 204 | 1,305 | 0 | 577 | |
| Y51 | 5,923 | -5.4 (3.6) | -2.9 (3.0) | 6.9 (1.9) | 2.5 (2.0) |
| Unknown | 222 | 1,279 | 0 | 576 | |
| Y52 | 5,966 | 32 (5) | -8 (3) | 26 (3) | -6 (3) |
| Unknown | 209 | 1,283 | 0 | 542 | |
| Y53 | 6,024 | 35 (6) | -6 (3) | 44 (6) | -3 (2) |
| Unknown | 184 | 1,243 | 0 | 549 | |
| Y54 | 5,953 | 34 (6) | -5 (3) | 55 (7) | -1 (2) |
| Unknown | 217 | 1,281 | 0 | 549 | |
| Y55 | 5,950 | 35 (6) | -2 (2) | 62 (9) | -2 (2) |
| Unknown | 207 | 1,292 | 0 | 551 | |
| 1 Mean (SD); n / N (%) | |||||
Missingness Heatmap
cluster_heatmap(
data = df_missing,
clusters = paste0("Cluster ", clusters$clusters), ## Adds 'Cluster' to the cluster label
cols_ignore = "index",
observed_color = "#23013aff", ## A dark purple
missing_color = "yellow")## `use_raster` is automatically set to TRUE for a matrix with more than
## 2000 columns You can control `use_raster` argument by explicitly
## setting TRUE/FALSE to it.
##
## Set `ht_opt$message = FALSE` to turn off this message.## 'magick' package is suggested to install to give better rasterization.
##
## Set `ht_opt$message = FALSE` to turn off this message.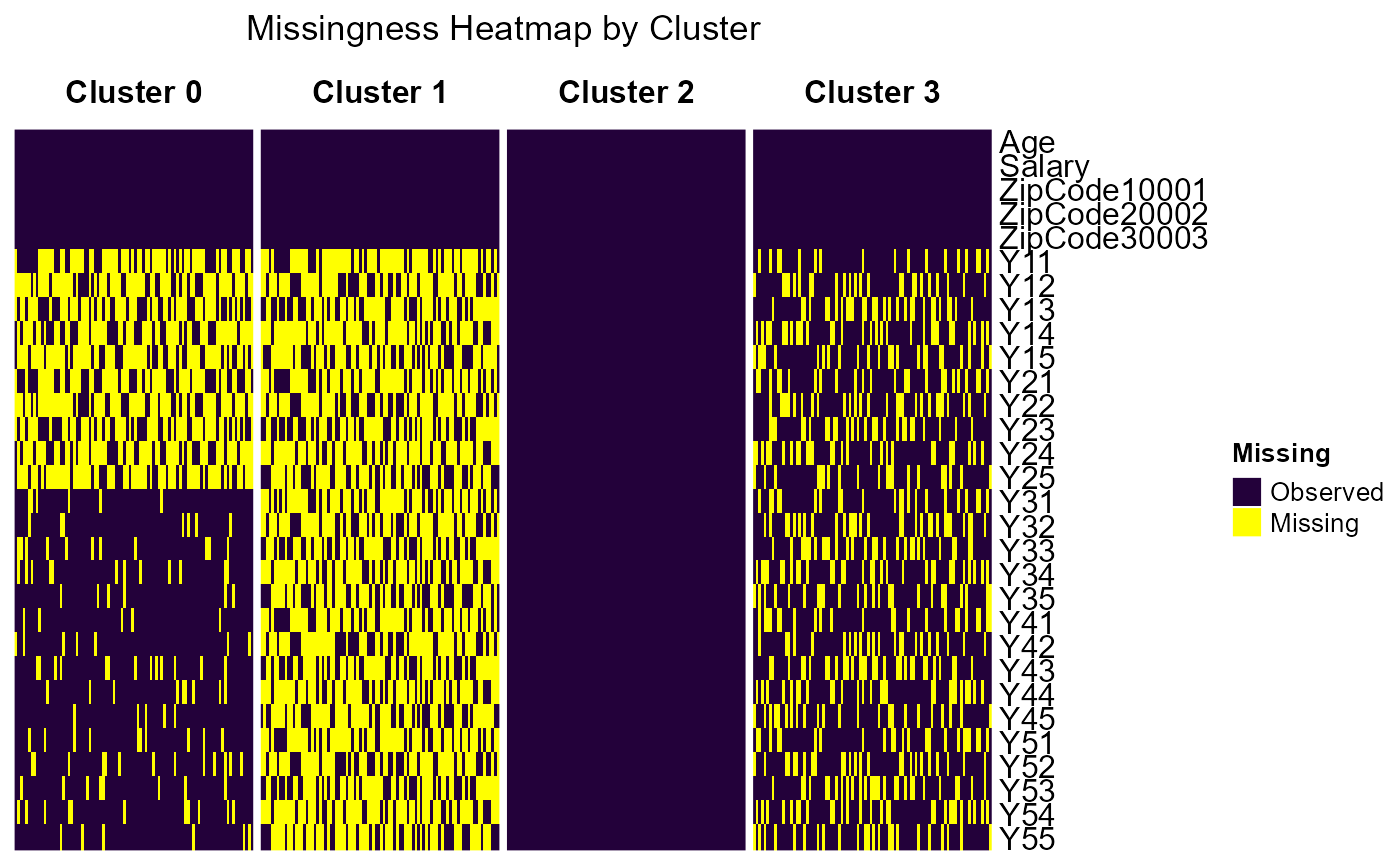
By-cluster imputation loss function
After running the model, you can get the per-cluster validation set
imputation loss using the performance_by_cluster()
function. Set ‘return_validation_dataset = TRUE’ in the
run_cissvae() function to be able to use
performance_by_cluster on the result object. If the validation dataset
(val_data in result object) and imputed validation dataset (val_imputed
in the result object) are not returned, the imputation loss cannot be
calculated.
If the run_cissvae() function was used to generate
clusters, set return_clusters=TRUE and the clusters will be
part of the return object. Otherwise, use the ‘clusters’ parameter in
performance_by_cluster() to input the clusters.
result = run_cissvae(
data = df_missing,
index_col = "index",
val_proportion = 0.1, ## pass a vector for different proportions by cluster
columns_ignore = c("Age", "Salary", "ZipCode10001", "ZipCode20002", "ZipCode30003"), ## If there are columns in addition to the index you want to ignore when selecting validation set, list them here. In this case, we ignore the 'demographic' columns because we do not want to remove data from them for validation purposes.
clusters = clusters$clusters, ## we have precomputed cluster labels so we pass them here
epochs = 5,
return_silhouettes = FALSE,
return_history = TRUE, # Get detailed training history
verbose = FALSE,
return_model = TRUE, ## Allows for plotting model schematic
device = "cpu", # Explicit device selection
layer_order_enc = c("unshared", "shared", "unshared"),
layer_order_dec = c("shared", "unshared", "shared"),
return_validation_dataset = TRUE
)
cat(paste("Check necessary returns:", paste0(names(result), collapse = ", ")))## Check necessary returns: imputed_dataset, model, training_history, val_data, val_imputed
performance_by_cluster(res = result,
group_col = NULL,
clusters = clusters$clusters,
feature_cols = NULL, ## default, all numeric columns excluding group_col & cols_ignore
by_group = FALSE,
by_cluster = TRUE,
cols_ignore = c( "index", "Age", "Salary", "ZipCode10001", "ZipCode20002", "ZipCode30003") ## columns to not score
)## $overall
## metric n
## 1 90.99783 13783
##
## $per_cluster
## cluster mean_imputation_loss n
## 1 0 48.70336 3408
## 2 1 96.68600 1787
## 3 2 80.57138 5000
## 4 3 142.86713 3588
##
## $per_feature_overall
## feature type mean_imputation_loss n
## 1 Y11 continuous 41.565153 486
## 2 Y12 continuous 89.328866 486
## 3 Y13 continuous 119.401816 488
## 4 Y14 continuous 160.124733 486
## 5 Y15 continuous 252.965269 484
## 6 Y21 continuous 66.576460 485
## 7 Y22 continuous 137.619200 489
## 8 Y23 continuous 127.223039 489
## 9 Y24 continuous 202.076766 484
## 10 Y25 continuous 234.807206 488
## 11 Y31 continuous 47.142491 592
## 12 Y32 continuous 87.786836 593
## 13 Y33 continuous 146.073318 597
## 14 Y34 continuous 168.344495 593
## 15 Y35 continuous 205.363351 593
## 16 Y41 continuous 7.179157 596
## 17 Y42 continuous 18.288482 596
## 18 Y43 continuous 37.223463 597
## 19 Y44 continuous 47.033124 597
## 20 Y45 continuous 61.172087 590
## 21 Y51 continuous 5.400970 591
## 22 Y52 continuous 19.634923 595
## 23 Y53 continuous 24.613987 601
## 24 Y54 continuous 26.400094 594
## 25 Y55 continuous 37.428103 593